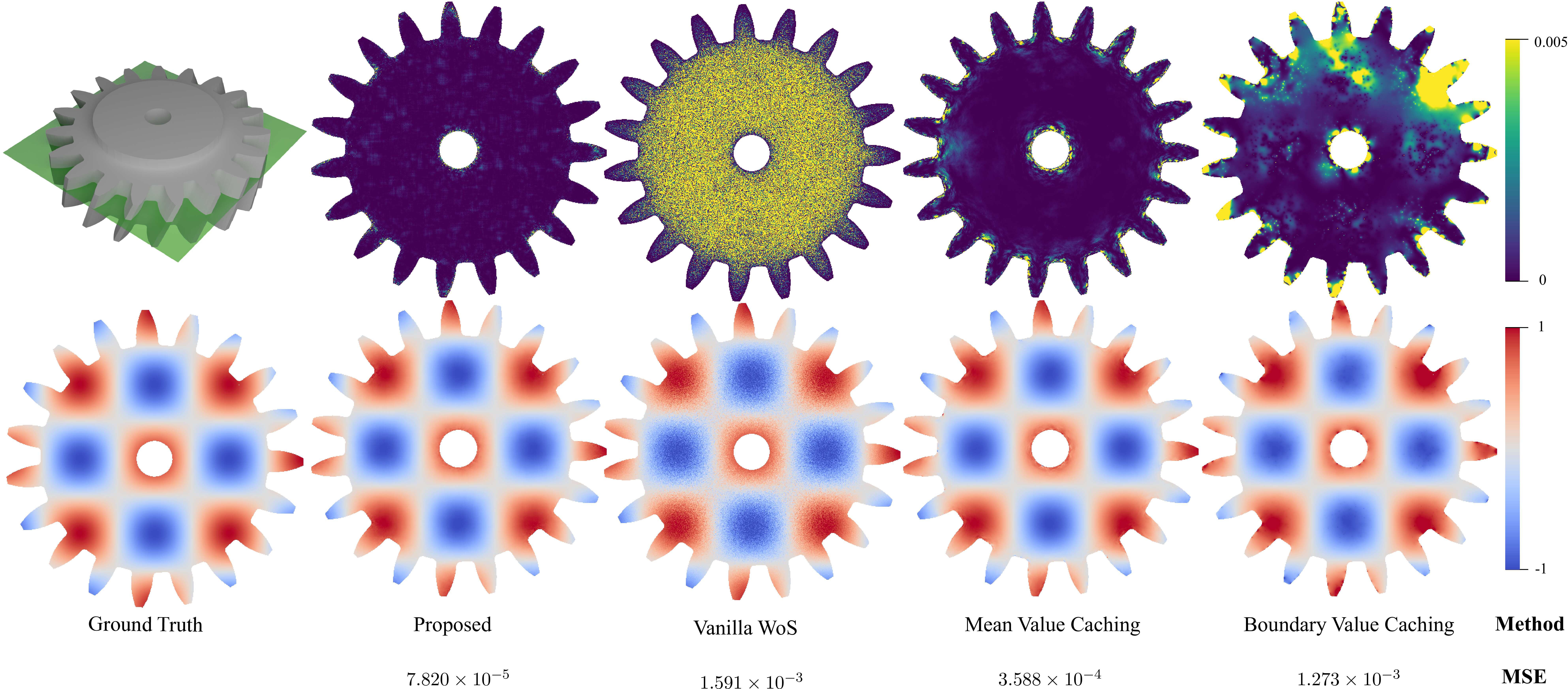
We propose a statistical weighting strategy for off-centered Monte Carlo estimators, demonstrating remarkable variance reduction results. The first row demonstrates error maps, and the results are shown in the second row. Compared with both vanilla walk on sphere algorithm and different variance reduction methods, our method reaches better mean square error within the same time.

Abstract

Stochastic PDE solvers have emerged as a powerful alternative to traditional discretization-based methods for solving partial differential equations (PDEs), especially in geometry processing and graphics. While off-centered estimators enhance sample reuse in WoS-type Monte Carlo solvers, they introduce correlation artifacts and bias when Green’s functions are approximated. In this paper, we propose a statistically weighted off-centered WoS-type estimator that leverages local similarity filtering to selectively combine samples across neighboring evaluation points. Our method balances bias and variance through a principled weighting strategy that suppresses unreliable estimators. We demonstrate our approach’s effectiveness on various PDEs—including screened Poisson equations—and boundary conditions, achieving consistent improvements over existing solvers such as vanilla Walk on Spheres, mean value caching, and boundary value caching. Our method also naturally extends to gradient field estimation and mixed boundary problems.

Implementation

Code: Github