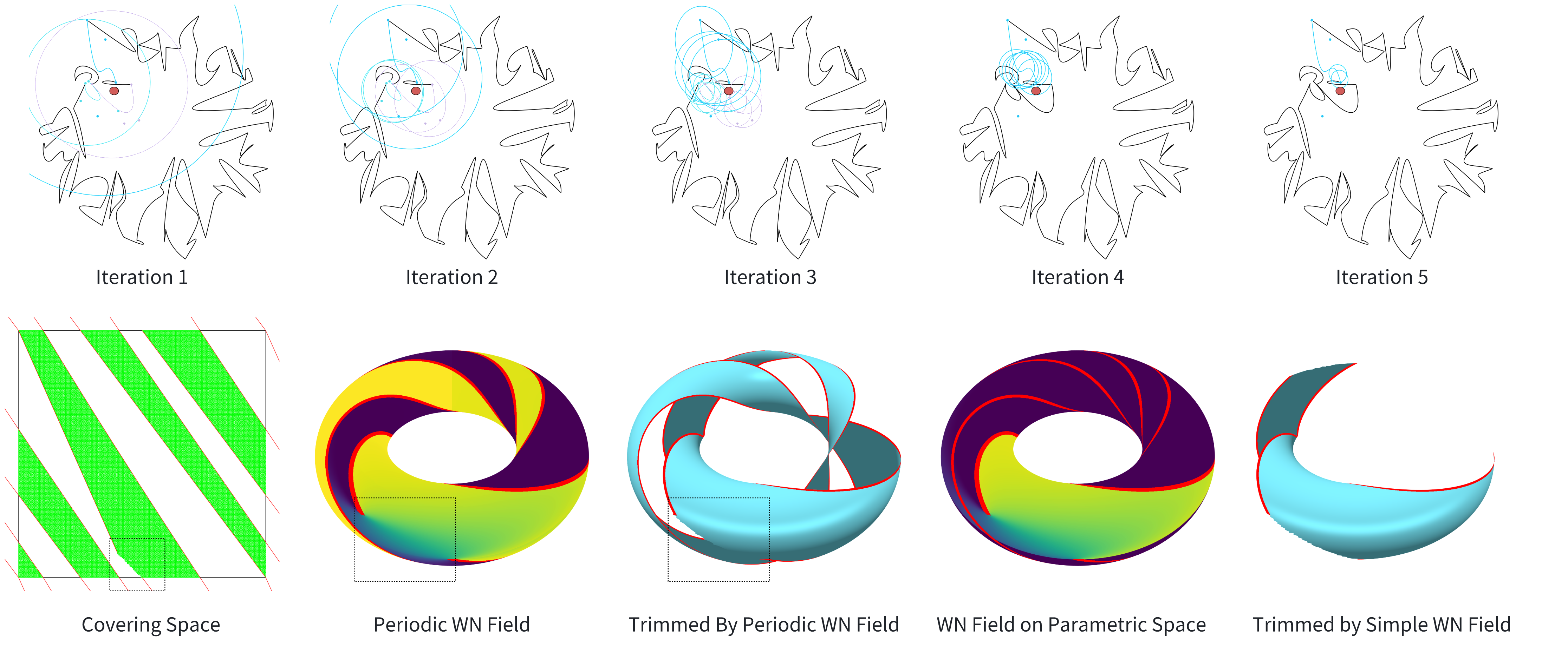
Caption: First row: Illustration of the winding number computation method. The red point is the testing point and the colored curves are ellipses used in our algorithms. Different from the [Spainhour et.al. 2024], we utilize a more flexible ellipse bound, enabling linear time Bezier curves evaluation and $O(1)$ inclusion test. Second row: By lifting curves to the universal covering space, we correctly compute the winding number on the periodic domain.

Abstract

Point containment queries on trimmed surfaces are fundamental to CAD modeling, solid geometry processing, and surface tessellation. Existing approaches—such as ray casting and generalized winding numbers—often face limitations in robustness and computational efficiency.

We propose a fast and numerically stable method for performing containment queries on trimmed surfaces, including those with periodic parameterizations. Our approach introduces a recursive winding number computation scheme that replaces costly curve subdivision with an ellipse-based bound for Bézier segments, enabling linear-time evaluation. For periodic surfaces, we lift trimming curves to the universal covering space, allowing accurate and consistent winding number computation even for non-contractible or discontinuous loops in parameter domain.

Experiments show that our method achieves substantial speedups over existing winding-number algorithms while maintaining high robustness in the presence of geometric noise, open boundaries, and periodic topologies. We further demonstrate its effectiveness in processing real B-Rep models and in robust tessellation of trimmed surfaces.